Loner John 的博客
0%

Closest pair of points-最近点问题-算法系列NO.1

发表于 更新于 分类于 ， Valine：

题目

Given a set S of n points in the plane (n is power of 2), c1=(x1, y1), c2=(x2, y2), …, cn=(xn, yn), where the points are ordered in ascending order of their x coordinates, find a pair points with closed instance.

给出一组点c1=(x1, y1), c2=(x2, y2), …, cn=(xn, yn)，找出他们之间距离最近的两个点，其中点ci的坐标xi按升序排列。

解题思路

对与这个问题，显然无脑解法是将S中每个点做两两对比，复杂度为O(n^2)。所以现在的目标是降低复杂度。

1.尝试使用分治法将问题缩小化
以x=c为界将点集S分为S1,S2。

2.尝试使用递归解决问题
目前距离最小的点p1,p2只可能有三种分布情况。
p1,p2都在S1中
p1,p2都在S2中
p1,p2分别在S1,S2中

于是问题简化变成了在S1,S2区域里寻找最短的距离d1,d2，寻找相邻区域中最短的距离d3。这里可以观察到，问题变小了。我们将点集S缩小为了S1,S2。这个问题可以应用递归来解决。

所以现在假设d1,d2 是可以求得的（别问，问就是要相信递归），那么问题简化为 已知d1,d2 求d3。

此时如果将S1中的所有点与S2中的所有点做两两比较，时间复杂度和题头写的无脑解法没区别了。那么现在的问题简化为想个方法减少计算的点的数目。

令d=min(d1,d2) 可以观察到只有距离x=c小于d的点之间的距离才可能小于d。只需取(c-d,x+d)之间的点进行计算。同理对于p(x1,y1)∈S1，q(x2,y2)∈S2。只需取|y2-y1|小于d的点进行计算。即只需计算在d x 2d范围内的点。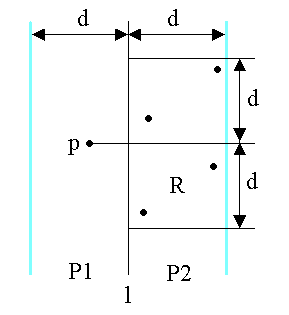
计算出d3的值后，S中点的最短距离为d=min(d3,d1,d2)

3.复杂度分析
证明d x 2d中最多只能有6个点：

1
2
将d x 2d分为六块等大矩形，每块矩形大小为d/2 x 2d/3 在每块矩形中斜边距离为5d/6 < d。
即每块矩形中最多只能存在一个点。

复杂度为： 6 x n/2 = 3n
可得出T(n)的表达式：
即：总时间复杂度为：T(n)=O(nlogn)

4.伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
getClosestPairDistances(S){
	n=S.lenth();
	if (n < 2) return flag;
/*Use x=c to construct S1 and S2, where c is the median of all x coordinates in S*/；
	S1={p∈S|x(p)<=c}, 
	S2={q∈S|x(q)>c};
	d1=getClosestPairDistances(S1);
    d2=getClosestPairDistances(S2);
	if(d1=flag&&d2=flag){
		return getDistance(p,q);
	}
	else if(d1=flag&&d2!=flag){d1=d2}
	else if(d2=flag&&d1!=flag){d2=d1}
	d=min(d1,d2);

	for(p : S1){
		if(x(p)-c<=d){
			for(q : S2){
				if(|y(q)-y(p)|<=d){
					if(getdistance(p,q)<d)d=getdistance(p,q);
				}
			}
		}
	}
	return d;
}

Java解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import java.awt.Point;
import java.util.*;

public class NO1 {
    /*
     * 递归算法求最短距离 */
    public double getClosestPairDistances(List<Point> S) {
        int length = S.size();
        if (length < 2) return -1;

        double c = S.get((length - 1) / 2).getX();
        List<Point> S1 = S.subList(0, (length + 1) / 2);
        List<Point> S2 = S.subList((length + 1) / 2, length);
        double d1 = getClosestPairDistances(S1);
        double d2 = getClosestPairDistances(S2);
        if (d1 == -1 && d2 == -1) {
            return S1.get(0).distance(S2.get(0));
        } else if (d1 == -1 || d2 == -1) {
            d1 = d2 = Double.max(d1, d2);
        }
        double d = Double.min(d1, d2);

        for (Point p : S1) {
            if (c - p.getX() <= d) {
                for (Point q : S2) {
                    if (-d <= p.getY() - q.getY() || p.getY() - q.getY() <= d) {
                        d = Double.min(p.distance(q), d);
                    }
                }
            }
        }
        return d;
    }

    public static void main(String[] args) {
        /*
         * 生成符合题干要求的点集 S */
        ArrayList<Point> list = new ArrayList<>();
        for (int i = 0; i < 20; i++) {
            list.add(new Point(new Random().nextInt(100), new Random().nextInt(100)));
        }
        list.sort(Comparator.comparingDouble(Point::getX));
        
        System.out.println(new NO1().getClosestPairDistances(list));
    }
}

C++解决

1
任性不想写了